la base - Funzione di Lagrange
Funzione di Lagrange
Menu principale:
la base
La base delle funzioni
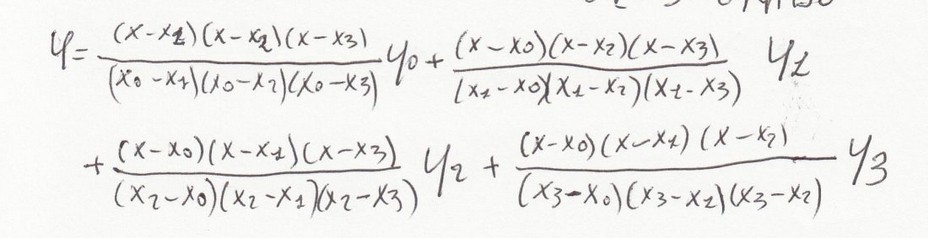
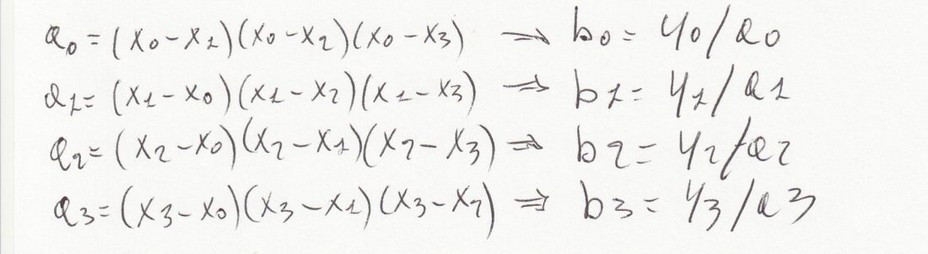
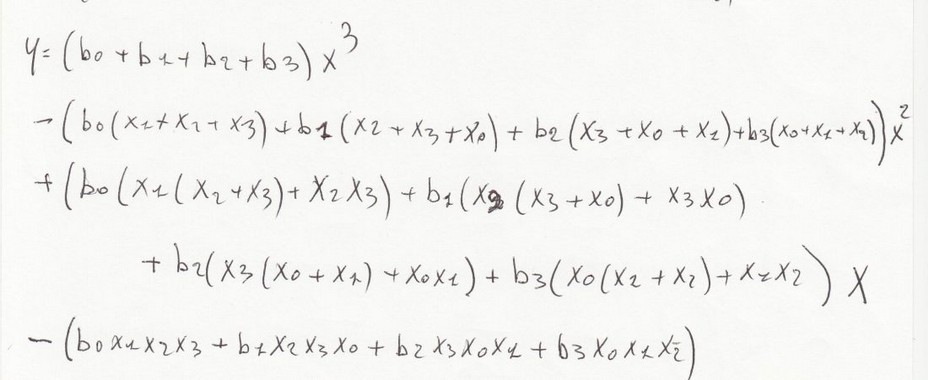
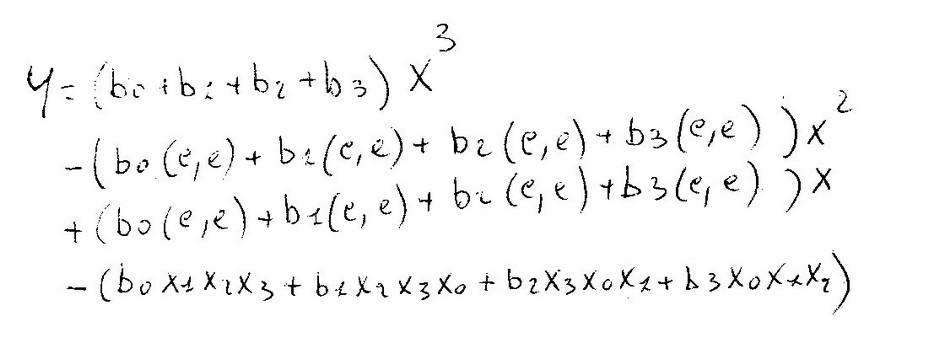
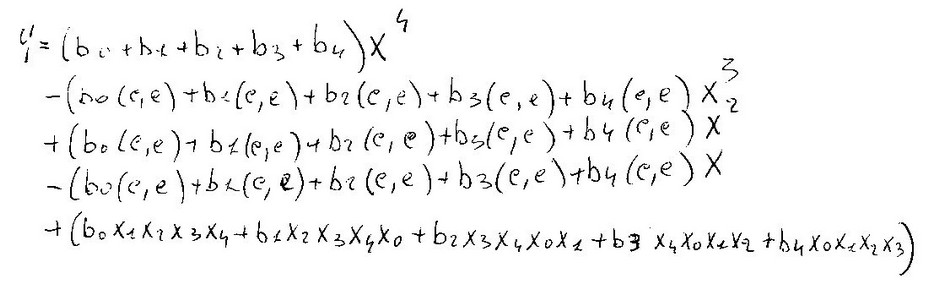
Anche per Lagrange la base della funzione sono come le fondamenta per una casa.
Prendiamo in considerazione la funzione di terzo grado, vedi sotto.
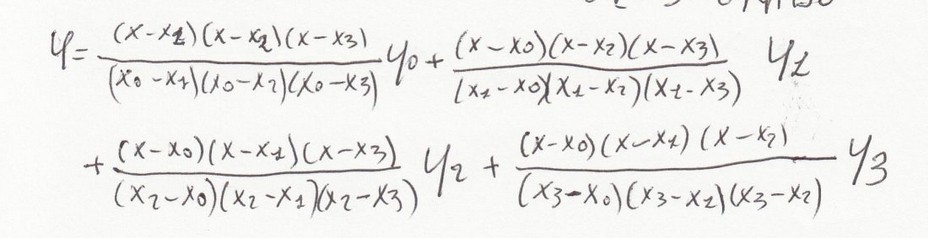
Dalla formula si può notare immediatamente che nella parte inferiore delle frazioni non vi sono variabili.
Per cui possiamo indicarle con delle a come si vede sotto.
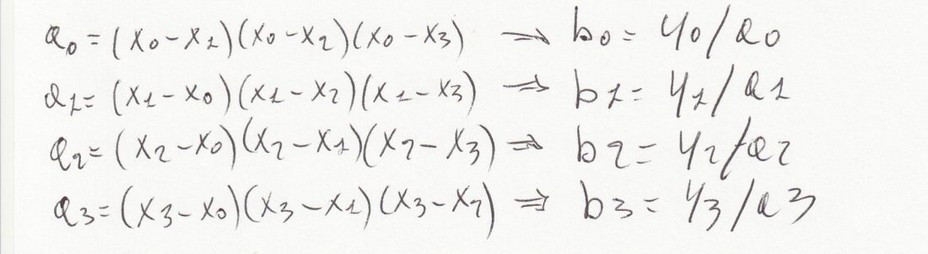
A questo punto occorre verificare se le a così ottenute sono "ricorsive". E così è. Anche in questo caso
con due semplici For-Next, uno per le x e uno per a, si possono calcolare le a sino al 99°, basta che
nel For-Next si esclude sestesso. Una volta calcolate le a si possono calcolare le b, sino al 99°.
Ora se nella formula di partenza effettuiamo la sostituzione, inserendo b, e facciamo lo svolgimento
otteniamo la formula mostrata sotto.
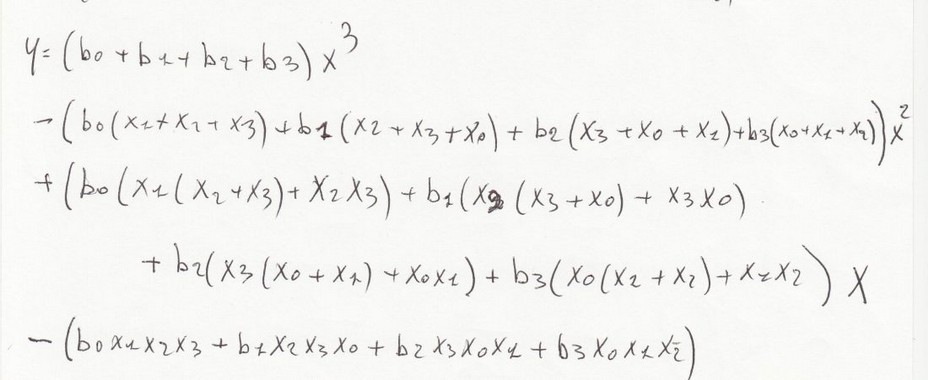
Ora, come con Newton, inseriamo "c,e" e otteniamo la figura sotto.
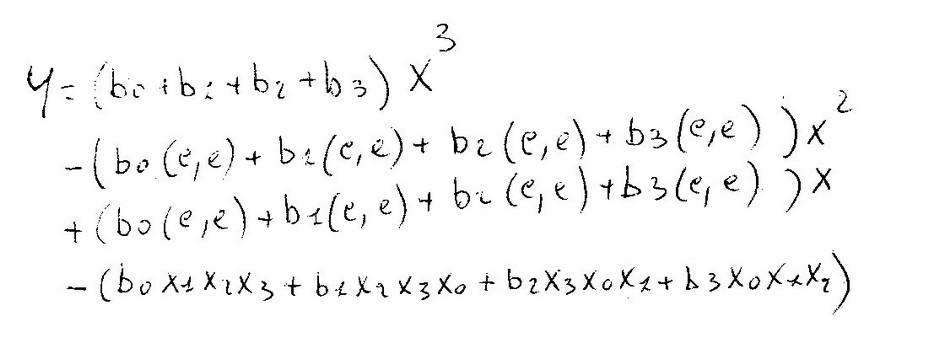
Anche con Lagrange la prima e l' ultima riga pur essendo "ricorsive" hanno regole dedicate, mente il "corpo"
ha una sola regola. La differenza con Newton è che si ottiene una "soluzione quadrata" al posto della
"soluzione triangolare", per il resto vale le stesse considerazioni.
Da notare che i segni sono "ricorsivi" ma seguono regole diverse da quelle di Newton.
Ora scriviamo la formula di grado superiore, cioè di quarto grado, senza effettuare lo svolgimento.
Con Newton si passava da a3_X^3 a a4_X^4 mentre ora da (b0+b1+b2+b3)X^3 si avrà
(b0+b1+b2+b3+b4)X^4 , si dovrà aumentare le b e l' esponente di X.
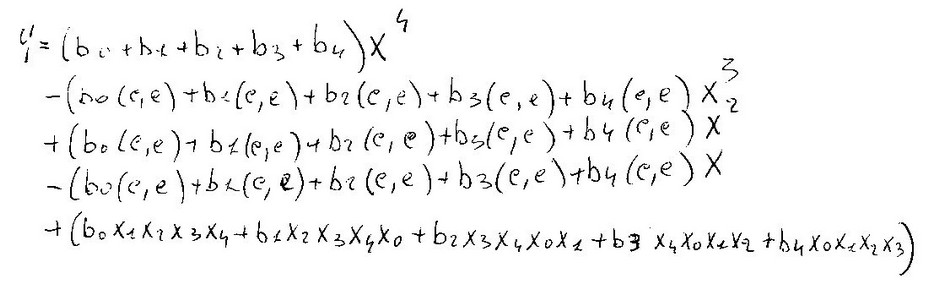
Con lo stesso metodo si scrive il "corpo" e l' ultima riga con il suo "ricorsivo".
Anche in questo caso, come con Newton, abbiamo la formula di grado superiore senza aver fatto nessun
svolgimento.
A questo punto con altri due For-Next, una per le righe e una per le colonne, come con Newton,
è possibile arrivare al 99°.