la tecnica - Funzione di Newton
Funzione Polimoniale di Newton a passo costante
Menu principale:
Approfondimento
Come arrivare
al listato "CombinazioneEquazionePassoCostante"
Per prima cosa occorre
analizzare il risultato della formula di
Newton correttamente raggruppata
secondo la teoria vista precedentemente (vedi sotto).
secondo la teoria vista precedentemente (vedi sotto).
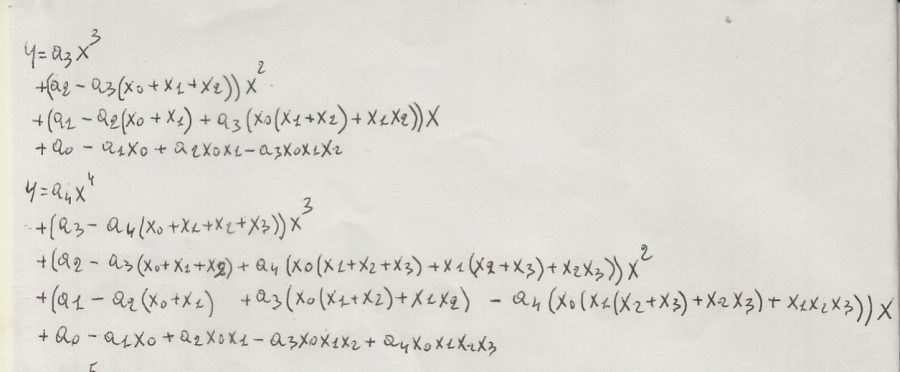
Nella figura di sopra si può notare le formule di Newton di terzo e quarto grado.
Analizzando le formule si possono fare due considerazioni, che ad un programmatore sembrano evidenti.
La prima : che le formule sono "ricorsive", si allargano come un "palloncino".
La seconda : che sono tutte combinazioni da due, concatenate come delle scatole cinesi.
Ora programmiamo la funzione di quarto grado, si avrà.
------------------------------------------------------------------
Private Sub Equazione_4G_PC()
On Error GoTo Next1
tz = tX2 + tX2 - tX1
If tz <> tX3 Then GoTo Next1
tz = tX3 + tX2 - tX1
If tz <> tX4 Then GoTo Next1
tyi0 = tY1
tyi1 = tY2
tyi2 = tY3
tyi3 = tY4
tyi4 = tY5
''''''''''''''''''
tdi3 = tyi4 - tyi3
tdi2 = tyi3 - tyi2
tdi1 = tyi2 - tyi1
tdi0 = tyi1 - tyi0
''''''''''''''''''
tdi3 = tdi3 - tdi2
tdi2 = tdi2 - tdi1
tdi1 = tdi1 - tdi0
''''''''''''''''''
tdi3 = tdi3 - tdi2
tdi2 = tdi2 - tdi1
''''''''''''''''''
tdi3 = tdi3 - tdi2
''''''''''''''''''
txi0 = tX1
txi1 = tX2
txi2 = tX3
txi3 = tX4
''''''''''''''''''
th = tX2 - tX1
''''''''''''''''''
tai0 = tY1
tai1 = tdi0 / th
tai2 = tdi1 / (1 * 2 * th ^ 2)
tai3 = tdi2 / (1 * 2 * 3 * th ^ 3)
tai4 = tdi3 / (1 * 2 * 3 * 4 * th ^ 4)
''''''''''''''''''''''''''''''''''''''
ta = tai4
tb = tai3 - tai4 * (txi0 + txi1 + txi2 + txi3)
tc = tai2 - tai3 * (txi0 + txi1 + txi2) + tai4 * (txi0 * txi1 + txi0 * txi2 + txi0 * txi3 + txi1 * txi2 + txi1 * txi3 + txi2 * txi3)
td = tai1 - tai2 * (txi0 + txi1) + tai3 * (txi0 * txi1 + txi0 * txi2 + txi1 * txi2)
- tai4 * (txi0 * txi1 * txi2 + txi0 * txi1 * txi3 + txi0 * txi2 * txi3 + txi1 * txi2 * txi3)
te = tai0 - tai1 * txi0 + tai2 * txi0 * txi1 - tai3 * txi0 * txi1 * txi2 + tai4 * txi0 * txi1 * txi2 * txi3
'''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
Exit Sub
Next1:
picGlobo.Picture = LoadPicture("C:\MSG\MSG_INI\MSG_Palette.gif")
End Sub
-------------------------------------------------------------------------
On Error GoTo Next1
tz = tX2 + tX2 - tX1
If tz <> tX3 Then GoTo Next1
tz = tX3 + tX2 - tX1
If tz <> tX4 Then GoTo Next1
tyi0 = tY1
tyi1 = tY2
tyi2 = tY3
tyi3 = tY4
tyi4 = tY5
''''''''''''''''''
tdi3 = tyi4 - tyi3
tdi2 = tyi3 - tyi2
tdi1 = tyi2 - tyi1
tdi0 = tyi1 - tyi0
''''''''''''''''''
tdi3 = tdi3 - tdi2
tdi2 = tdi2 - tdi1
tdi1 = tdi1 - tdi0
''''''''''''''''''
tdi3 = tdi3 - tdi2
tdi2 = tdi2 - tdi1
''''''''''''''''''
tdi3 = tdi3 - tdi2
''''''''''''''''''
txi0 = tX1
txi1 = tX2
txi2 = tX3
txi3 = tX4
''''''''''''''''''
th = tX2 - tX1
''''''''''''''''''
tai0 = tY1
tai1 = tdi0 / th
tai2 = tdi1 / (1 * 2 * th ^ 2)
tai3 = tdi2 / (1 * 2 * 3 * th ^ 3)
tai4 = tdi3 / (1 * 2 * 3 * 4 * th ^ 4)
''''''''''''''''''''''''''''''''''''''
ta = tai4
tb = tai3 - tai4 * (txi0 + txi1 + txi2 + txi3)
tc = tai2 - tai3 * (txi0 + txi1 + txi2) + tai4 * (txi0 * txi1 + txi0 * txi2 + txi0 * txi3 + txi1 * txi2 + txi1 * txi3 + txi2 * txi3)
td = tai1 - tai2 * (txi0 + txi1) + tai3 * (txi0 * txi1 + txi0 * txi2 + txi1 * txi2)
- tai4 * (txi0 * txi1 * txi2 + txi0 * txi1 * txi3 + txi0 * txi2 * txi3 + txi1 * txi2 * txi3)
te = tai0 - tai1 * txi0 + tai2 * txi0 * txi1 - tai3 * txi0 * txi1 * txi2 + tai4 * txi0 * txi1 * txi2 * txi3
'''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
Exit Sub
Next1:
picGlobo.Picture = LoadPicture("C:\MSG\MSG_INI\MSG_Palette.gif")
End Sub
-------------------------------------------------------------------------
Ora prendiamo in
conziderasione la quarta riga della funzione
di quarto grado, essa è.
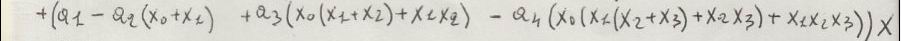
che programmata :
td = tai1 - tai2 * (txi0 + txi1) + tai3 * (txi0 * txi1 + txi0 * txi2 + txi1 * txi2)
- tai4 * (txi0 * txi1 * txi2 + txi0 * txi1 * txi3 + txi0 * txi2 * txi3 + txi1 * txi2 * txi3)
Non analizzamo la prima e la seconda colonna, perchè, come gia visto, sono colonne anomale, ma prendiamo in
cosiderazione solo la terza colonna.
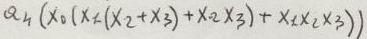
che programmata risulta.
tai4 * (txi0 * txi1 * txi2 + txi0 * txi1 * txi3 + txi0 * txi2 * txi3 + txi1 * txi2 * txi3)
Analizziamo il cuore di questa combinazione, a4(3,4).
X1(X2 + X3)
Programmiamo questa formula, combinazione da due con un numero di elementi X,
in questo caso due.
Private Sub Comb2ElemX()
On Error GoTo NextErr
tC2EX = 0
For J = J1 + 1 To nElem
tC1EX = 0
For W = J To nElem
tC1EX = tC1EX + txin(W)
Next
tC2EX = tC2EX + txin(J - 1) * tC1EX
Next
Exit Sub
NextErr:
EQZ_Err = -1
End Sub
Come si può notare.
tC1EX = tC1EX + txin(W)
fa la somma degli elementi, in questo caso X2 + X3.
Mentre
txin(J - 1) * tC1EX
fa la moltiplicazione, calcolando così, X1(X2 + X3).
Ora prendiamo di nuovo in considerazione la terza colonna.
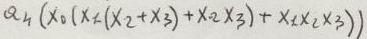
che programmata si ottiene.
tai4 * (txi0 * txi1 * txi2 + txi0 * txi1 * txi3 + txi0 * txi2 * txi3 + txi1 * txi2 * txi3)
Non considerando a4.
txi0 * txi1 * txi2 + txi0 * txi1 * txi3 + txi0 * txi2 * txi3 + txi1 * txi2 * txi3
da cui.
txi0*(txi1*(txi2 + txi3) + txi2*txi3) + txi1*txi2*txi3
programmandola, con dei for-next, si ottiene.
tC4EX = 0
For J2 = 1 To nElem - nComb + 2
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 3
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tCEPC = tC4EX
Exit Sub
Per ottenere questo listato occorre considerare che sono tutte combiazione da due concatenate.
Come visto precedentemente: nComb = numero delle combinazioni
nElem = numero degli elementi
Il cuore del listato è, Call Comb2ElemX, come visto prima.
Mentre il resto lo si concatena con dei for-next, facendoli partire e arrivare in modo appropriato.
Per cui entra in gioco, J2 = 1 e J1 = J2 + 1, elementi di partenza e, nElem - nComb + 2, e
nElem - nComb + 3, elementi di arrivo, che devono tener conto della generalità.
Il listato deve essere a carattere generale, perchè deve arrivare al 99° grado, e oltre.
Compreso questo passaggio, si arriva al listato sotto, che calcola le funzioni sino al decimo grado.
che programmata :
td = tai1 - tai2 * (txi0 + txi1) + tai3 * (txi0 * txi1 + txi0 * txi2 + txi1 * txi2)
- tai4 * (txi0 * txi1 * txi2 + txi0 * txi1 * txi3 + txi0 * txi2 * txi3 + txi1 * txi2 * txi3)
Non analizzamo la prima e la seconda colonna, perchè, come gia visto, sono colonne anomale, ma prendiamo in
cosiderazione solo la terza colonna.
che programmata risulta.
tai4 * (txi0 * txi1 * txi2 + txi0 * txi1 * txi3 + txi0 * txi2 * txi3 + txi1 * txi2 * txi3)
Analizziamo il cuore di questa combinazione, a4(3,4).
X1(X2 + X3)
Programmiamo questa formula, combinazione da due con un numero di elementi X,
in questo caso due.
Private Sub Comb2ElemX()
On Error GoTo NextErr
tC2EX = 0
For J = J1 + 1 To nElem
tC1EX = 0
For W = J To nElem
tC1EX = tC1EX + txin(W)
Next
tC2EX = tC2EX + txin(J - 1) * tC1EX
Next
Exit Sub
NextErr:
EQZ_Err = -1
End Sub
Come si può notare.
tC1EX = tC1EX + txin(W)
fa la somma degli elementi, in questo caso X2 + X3.
Mentre
txin(J - 1) * tC1EX
fa la moltiplicazione, calcolando così, X1(X2 + X3).
Ora prendiamo di nuovo in considerazione la terza colonna.
che programmata si ottiene.
tai4 * (txi0 * txi1 * txi2 + txi0 * txi1 * txi3 + txi0 * txi2 * txi3 + txi1 * txi2 * txi3)
Non considerando a4.
txi0 * txi1 * txi2 + txi0 * txi1 * txi3 + txi0 * txi2 * txi3 + txi1 * txi2 * txi3
da cui.
txi0*(txi1*(txi2 + txi3) + txi2*txi3) + txi1*txi2*txi3
programmandola, con dei for-next, si ottiene.
tC4EX = 0
For J2 = 1 To nElem - nComb + 2
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 3
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tCEPC = tC4EX
Exit Sub
Per ottenere questo listato occorre considerare che sono tutte combiazione da due concatenate.
Come visto precedentemente: nComb = numero delle combinazioni
nElem = numero degli elementi
Il cuore del listato è, Call Comb2ElemX, come visto prima.
Mentre il resto lo si concatena con dei for-next, facendoli partire e arrivare in modo appropriato.
Per cui entra in gioco, J2 = 1 e J1 = J2 + 1, elementi di partenza e, nElem - nComb + 2, e
nElem - nComb + 3, elementi di arrivo, che devono tener conto della generalità.
Il listato deve essere a carattere generale, perchè deve arrivare al 99° grado, e oltre.
Compreso questo passaggio, si arriva al listato sotto, che calcola le funzioni sino al decimo grado.
------------------------------------------------------------------
Private Sub CombinazioneEquazionePassoCostante()
'// Entrata nComb ////////////////////////////////////////////////////////////////////////
'// Entrata nElem ////////////////////////////////////////////////////////////////////////
'// Uscita tCEPC ////////////////////////////////////////////////////////////////////////
On Error GoTo NextErr
If nComb = 2 Then GoTo Next2
If nComb = 3 Then GoTo Next3
If nComb = 4 Then GoTo Next4
If nComb = 5 Then GoTo Next5
If nComb = 6 Then GoTo Next6
If nComb = 7 Then GoTo Next7
If nComb = 8 Then GoTo Next8
If nComb = 9 Then GoTo Next9
GoTo NextErr
''''''''''''''''''''''''''''''
''''' combinazione da 2 ''''''
''''''''''''''''''''''''''''''
Next2:
J1 = 0
Call Comb2ElemX
tCEPC = tC2EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 3 ''''''
''''''''''''''''''''''''''''''
Next3:
tC3EX = 0
For J1 = 1 To nElem - nComb + 2
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tCEPC = tC3EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 4 ''''''
''''''''''''''''''''''''''''''
Next4:
tC4EX = 0
For J2 = 1 To nElem - nComb + 2
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 3
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tCEPC = tC4EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 5 ''''''
''''''''''''''''''''''''''''''
Next5:
tC5EX = 0
For J3 = 1 To nElem - nComb + 2
tC4EX = 0
For J2 = J3 + 1 To nElem - nComb + 3
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 4
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tC5EX = tC5EX + txin(J3 - 1) * tC4EX
Next
tCEPC = tC5EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 6 ''''''
''''''''''''''''''''''''''''''
Next6:
tC6EX = 0
For J4 = 1 To nElem - nComb + 2
tC5EX = 0
For J3 = J4 + 1 To nElem - nComb + 3
tC4EX = 0
For J2 = J3 + 1 To nElem - nComb + 4
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 5
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tC5EX = tC5EX + txin(J3 - 1) * tC4EX
Next
tC6EX = tC6EX + txin(J4 - 1) * tC5EX
Next
tCEPC = tC6EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 7 ''''''
''''''''''''''''''''''''''''''
Next7:
tC7EX = 0
For J5 = 1 To nElem - nComb + 2
tC6EX = 0
For J4 = J5 + 1 To nElem - nComb + 3
tC5EX = 0
For J3 = J4 + 1 To nElem - nComb + 4
tC4EX = 0
For J2 = J3 + 1 To nElem - nComb + 5
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 6
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tC5EX = tC5EX + txin(J3 - 1) * tC4EX
Next
tC6EX = tC6EX + txin(J4 - 1) * tC5EX
Next
tC7EX = tC7EX + txin(J5 - 1) * tC6EX
Next
tCEPC = tC7EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 8 ''''''
''''''''''''''''''''''''''''''
Next8:
tC8EX = 0
For J6 = 1 To nElem - nComb + 2
tC7EX = 0
For J5 = J6 + 1 To nElem - nComb + 3
tC6EX = 0
For J4 = J5 + 1 To nElem - nComb + 4
tC5EX = 0
For J3 = J4 + 1 To nElem - nComb + 5
tC4EX = 0
For J2 = J3 + 1 To nElem - nComb + 6
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 7
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tC5EX = tC5EX + txin(J3 - 1) * tC4EX
Next
tC6EX = tC6EX + txin(J4 - 1) * tC5EX
Next
tC7EX = tC7EX + txin(J5 - 1) * tC6EX
Next
tC8EX = tC8EX + txin(J6 - 1) * tC7EX
Next
tCEPC = tC8EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 9 ''''''
''''''''''''''''''''''''''''''
Next9:
tC9EX = 0
For J7 = 1 To nElem - nComb + 2
tC8EX = 0
For J6 = J7 + 1 To nElem - nComb + 3
tC7EX = 0
For J5 = J6 + 1 To nElem - nComb + 4
tC6EX = 0
For J4 = J5 + 1 To nElem - nComb + 5
tC5EX = 0
For J3 = J4 + 1 To nElem - nComb + 6
tC4EX = 0
For J2 = J3 + 1 To nElem - nComb + 7
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 8
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tC5EX = tC5EX + txin(J3 - 1) * tC4EX
Next
tC6EX = tC6EX + txin(J4 - 1) * tC5EX
Next
tC7EX = tC7EX + txin(J5 - 1) * tC6EX
Next
tC8EX = tC8EX + txin(J6 - 1) * tC7EX
Next
tC9EX = tC9EX + txin(J7 - 1) * tC8EX
Next
tCEPC = tC9EX
Exit Sub
NextErr:
EQZ_Err = -1
End Sub
Private Sub Comb2ElemX()
On Error GoTo NextErr
tC2EX = 0
For J = J1 + 1 To nElem
tC1EX = 0
For W = J To nElem
tC1EX = tC1EX + txin(W)
Next
tC2EX = tC2EX + txin(J - 1) * tC1EX
Next
Exit Sub
NextErr:
EQZ_Err = -1
End Sub
'// Entrata nComb ////////////////////////////////////////////////////////////////////////
'// Entrata nElem ////////////////////////////////////////////////////////////////////////
'// Uscita tCEPC ////////////////////////////////////////////////////////////////////////
On Error GoTo NextErr
If nComb = 2 Then GoTo Next2
If nComb = 3 Then GoTo Next3
If nComb = 4 Then GoTo Next4
If nComb = 5 Then GoTo Next5
If nComb = 6 Then GoTo Next6
If nComb = 7 Then GoTo Next7
If nComb = 8 Then GoTo Next8
If nComb = 9 Then GoTo Next9
GoTo NextErr
''''''''''''''''''''''''''''''
''''' combinazione da 2 ''''''
''''''''''''''''''''''''''''''
Next2:
J1 = 0
Call Comb2ElemX
tCEPC = tC2EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 3 ''''''
''''''''''''''''''''''''''''''
Next3:
tC3EX = 0
For J1 = 1 To nElem - nComb + 2
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tCEPC = tC3EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 4 ''''''
''''''''''''''''''''''''''''''
Next4:
tC4EX = 0
For J2 = 1 To nElem - nComb + 2
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 3
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tCEPC = tC4EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 5 ''''''
''''''''''''''''''''''''''''''
Next5:
tC5EX = 0
For J3 = 1 To nElem - nComb + 2
tC4EX = 0
For J2 = J3 + 1 To nElem - nComb + 3
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 4
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tC5EX = tC5EX + txin(J3 - 1) * tC4EX
Next
tCEPC = tC5EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 6 ''''''
''''''''''''''''''''''''''''''
Next6:
tC6EX = 0
For J4 = 1 To nElem - nComb + 2
tC5EX = 0
For J3 = J4 + 1 To nElem - nComb + 3
tC4EX = 0
For J2 = J3 + 1 To nElem - nComb + 4
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 5
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tC5EX = tC5EX + txin(J3 - 1) * tC4EX
Next
tC6EX = tC6EX + txin(J4 - 1) * tC5EX
Next
tCEPC = tC6EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 7 ''''''
''''''''''''''''''''''''''''''
Next7:
tC7EX = 0
For J5 = 1 To nElem - nComb + 2
tC6EX = 0
For J4 = J5 + 1 To nElem - nComb + 3
tC5EX = 0
For J3 = J4 + 1 To nElem - nComb + 4
tC4EX = 0
For J2 = J3 + 1 To nElem - nComb + 5
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 6
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tC5EX = tC5EX + txin(J3 - 1) * tC4EX
Next
tC6EX = tC6EX + txin(J4 - 1) * tC5EX
Next
tC7EX = tC7EX + txin(J5 - 1) * tC6EX
Next
tCEPC = tC7EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 8 ''''''
''''''''''''''''''''''''''''''
Next8:
tC8EX = 0
For J6 = 1 To nElem - nComb + 2
tC7EX = 0
For J5 = J6 + 1 To nElem - nComb + 3
tC6EX = 0
For J4 = J5 + 1 To nElem - nComb + 4
tC5EX = 0
For J3 = J4 + 1 To nElem - nComb + 5
tC4EX = 0
For J2 = J3 + 1 To nElem - nComb + 6
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 7
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tC5EX = tC5EX + txin(J3 - 1) * tC4EX
Next
tC6EX = tC6EX + txin(J4 - 1) * tC5EX
Next
tC7EX = tC7EX + txin(J5 - 1) * tC6EX
Next
tC8EX = tC8EX + txin(J6 - 1) * tC7EX
Next
tCEPC = tC8EX
Exit Sub
''''''''''''''''''''''''''''''
''''' combinazione da 9 ''''''
''''''''''''''''''''''''''''''
Next9:
tC9EX = 0
For J7 = 1 To nElem - nComb + 2
tC8EX = 0
For J6 = J7 + 1 To nElem - nComb + 3
tC7EX = 0
For J5 = J6 + 1 To nElem - nComb + 4
tC6EX = 0
For J4 = J5 + 1 To nElem - nComb + 5
tC5EX = 0
For J3 = J4 + 1 To nElem - nComb + 6
tC4EX = 0
For J2 = J3 + 1 To nElem - nComb + 7
tC3EX = 0
For J1 = J2 + 1 To nElem - nComb + 8
Call Comb2ElemX
tC3EX = tC3EX + txin(J1 - 1) * tC2EX
Next
tC4EX = tC4EX + txin(J2 - 1) * tC3EX
Next
tC5EX = tC5EX + txin(J3 - 1) * tC4EX
Next
tC6EX = tC6EX + txin(J4 - 1) * tC5EX
Next
tC7EX = tC7EX + txin(J5 - 1) * tC6EX
Next
tC8EX = tC8EX + txin(J6 - 1) * tC7EX
Next
tC9EX = tC9EX + txin(J7 - 1) * tC8EX
Next
tCEPC = tC9EX
Exit Sub
NextErr:
EQZ_Err = -1
End Sub
Private Sub Comb2ElemX()
On Error GoTo NextErr
tC2EX = 0
For J = J1 + 1 To nElem
tC1EX = 0
For W = J To nElem
tC1EX = tC1EX + txin(W)
Next
tC2EX = tC2EX + txin(J - 1) * tC1EX
Next
Exit Sub
NextErr:
EQZ_Err = -1
End Sub
-----------------------------------------------------------
Dall' analisi del listato sopra, si può notare, che passare da una funzione di quarto grado a una
funzione di quinto grado occore semplicemente aggiungere un for-next.
Le combinazioni si allargano in modo lineare aggiungedo, via via, solo dei for-next.
Dal listato sopra si nota immediatamente, che occorre una serie di for-next per ogni grado.
Per cui per arrivare al 99° grado occorrono 99 serie di for-next, che si allargano in modo lineare.
Tutti sanno che, da un for-next si può uscire, ma non si puo entrare.
Un modo semplice per semplificare il sottoprogramma, è quello di tradurre il for-next in if.
Dall' if non solo si può uscire, ma anche entrare, semplificando notevolmente il programma.
Per passare dal for-next all' if occorre solo una semplice traduzione.
Ecco spiegato il sottoprogramma, "CombinazioneEquazionePassoCostante",
Dall' analisi del listato sopra, si può notare, che passare da una funzione di quarto grado a una
funzione di quinto grado occore semplicemente aggiungere un for-next.
Le combinazioni si allargano in modo lineare aggiungedo, via via, solo dei for-next.
Dal listato sopra si nota immediatamente, che occorre una serie di for-next per ogni grado.
Per cui per arrivare al 99° grado occorrono 99 serie di for-next, che si allargano in modo lineare.
Tutti sanno che, da un for-next si può uscire, ma non si puo entrare.
Un modo semplice per semplificare il sottoprogramma, è quello di tradurre il for-next in if.
Dall' if non solo si può uscire, ma anche entrare, semplificando notevolmente il programma.
Per passare dal for-next all' if occorre solo una semplice traduzione.
Ecco spiegato il sottoprogramma, "CombinazioneEquazionePassoCostante",
visto nel listato
della pagina precedente.