Funzione di Newton
Funzione Polimoniale di Newton a passo costante
Menu principale:
Come calcolare la funzione di Newton al 99° senza impazzire
Calcolare la funzione di Newton al novantanovesimo grado può sembrare una pazzia, ma non è così.
Per raggiungere questo obbiettivo occorre trovare una strada diversa da quella conosciuta.
Newton non aveva bisogno di trovare altre soluzioni perchè al suo tempo non esistevano i
computer ne i linguaggi di programmazione. Oggigiorno una formula matematica è veramente
utile se programmabile, semplicemente programmabile. Una formula difficilmente programmabile
porta ad un rallentamento del programma e una scarza utilità. Un programma veramente utile è
quello semplice e veloce, che comporta risultati eccezionali. Un esempio di questo sono proprio
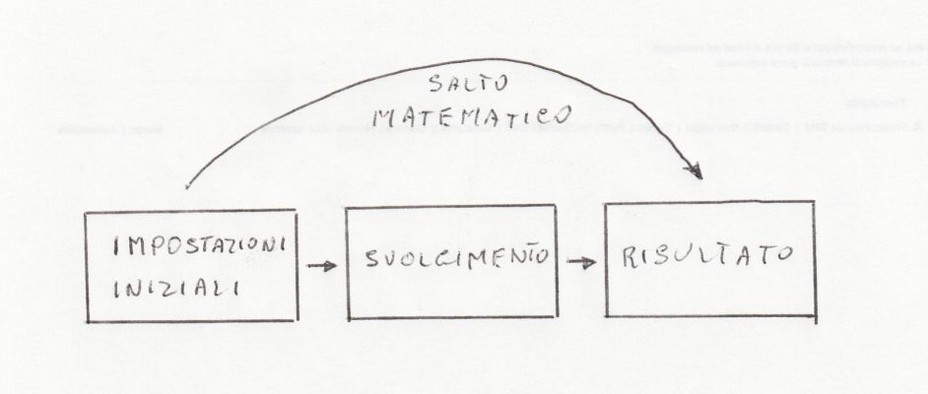
le Funzioni di Newton. Con la procedura sinora conosciuta, cioè effettuando lo svolgimento delle
impostazioni iniziali, porta ad una programmazione difficile per non dire impossibile.
Per questo motivo ho studiato un nuovo metodo, un pò più difficile dello svolgimento, ma porta
ad un programmazione semplice e veloce, arrivando ad altezze finora sconosciute.
Per arrivare al novantanovesimo grado occorrono quattro condizioni:
la prima : Il salto matematico
la seconda : il salto programmatico
la terza : la precisione (riferita al computer)
la quarta : la velocità (riferita al computer)
Le prime tre condizioni sono una realtà, la quarta ci stiamo organizzando.
Il salto matematico
Che cosa è il salto matematico?. Il salto matematico consiste nello scrivere il risultato senza effettuare
lo svolgimento. Questo può sembrare impossibile, e infatti lo è se si ha in mente il vecchio metodo.

Per poter capire il salto matematico occorre fare un esempio. Avete da piccoli gonfiato un palloncino
soffiandoci dentro. E dopo averlo gonfiato ci soffiate di nuovo, cosa succede?. Il palloncino si allarga
mantenendo invariata la forma, qualsiasi essa sia. Per cui si può vedere cosa sarà il palloncino prima di
averci soffiato dentro, perchè la forma che avrà è prevedibile. La stessa cosa vale per le funzioni di Newton.
All' aumentare dei gradi il risultato non è diverso, ma solo più grande. La struttura e tutto il resto rimane
invariata all' aumentare dei gradi, semplicemente più grande. Per cui, come nel palloncino, occorre capire
le regole del suo allargamento. Questo metodo io lo chiamato "ricorsivo" cioè "ricorrente" perchè si
allarga in modo prevedibile, come quando si conta i numeri da zero all' infinito. Contare i numeri da zero
all' infinito è possibile perchè il metodo è "ricorsivo".
Per capire le regole del salto matematico occorre studiarle in due fasi distinti.
Prima fase : La base.
Seconda fase : La tecnica delle combinazioni specifica per le funzioni.
Capite queste due fasi, si arriva ha capire il salto matematico.