conclusioni - Funzione di Newton
Funzione Polimoniale di Newton a passo costante
Menu principale:
conclusioni
Conclusioni
Visto le pagine precedente si può fare le seguenti conclusioni.
Come abbiamo detto nelle pagine precedenti è stato spiegato il "salto matematico".
Questo metodo è importante perchè si arriva a programmare le funzioni con grande semplicità.
Basti pensare che in Basic occorrono solo sei righe per ogni grado per calcolare la Funzione
di Newton, più il "corpo" che rimane invariato per qualsiasi grado.
Ecco perchè si può scrivere un programma sino al 99° grado. Ed è già stato scritto.
Ora occorre capire come arrivare a tale risultato.
Il salto programmatico
Se il risultato della formula di Newton, come visto precedentemente, è "ricorsivo" si presuppone
che una volta programmato, anche il programma risulta "ricorsivo". E infatti così è.
Il risultato della formula di Newton anche con il metodo "ricorsivo" non è possibile scriverlo
molto superiore al metodo tradizionale, per cui occorre di nuovo trovare un' altra strada.
Trovate le regole del metodo "ricorsivo" del programma si può scrivere il programma saltando
sia lo svolgimento, sia il risultato stesso, andando avanti semplicemente con la programmazione.
Spiegato così il salto programmatico, è possibile arrivare a 99° grado.
Precisione
Come già fatto notare precedentemente, pur avendo un programma sino al 99°, non è possibile
superare il quattordicesimo grado a causa degli errori commessi dal computer, nonostante tutte
le precauzioni prese. Anche in questo caso occorre trovare un' altra strada.
Un modo per arrivare al 35° è quello di passare dagli attuali 64 bit a 128 bit.
Questo oggigiorno lo si può fare in via software, per esempio programmando una opportuna
DLL che mi svolga questo lavoro, vedi sotto .
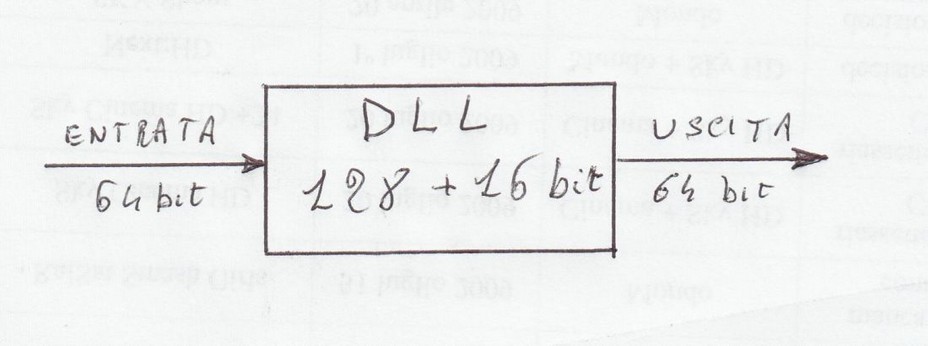
Come vedete la dll dovrebbe essere di 128 più sedici, dove 128 sono i numeri di bit di calcolo e
16 l' esponente. Non si deve strutturare il dato come in BASIC perchè non si arriva al 35°.
I segni del numero e dell' esponente dovrebbe essere il 15esimo e 14esimo dell' esponente,
per cui l' esponente potrebbe arrivare al massimo a 16383.
Questo metodo oltre ad avere una precisione superiore è anche più veloce (l' aumento di
velocità lo si può capire solo lavorando con il liguaggio macchina).
Come si vede un linguaggio di programmazione, per esempio BASIC, invia alla dll una serie di
dati a 64 bit e li riceve processati a 64 bit, non sapendo se sono stati elaborati a 64 o 128 bit.
Il metodo è semplice, la dll riceve i dati a 64 bit li converte a 128+16 bit li elabora e li converte
di nuovo a 64 bit, utili per qualsiasi elaborazione successiva.
Ora vediamo l' utilità di operare a 128+16 bit. I dati a 128+16 bit sono strutturati come sotto.
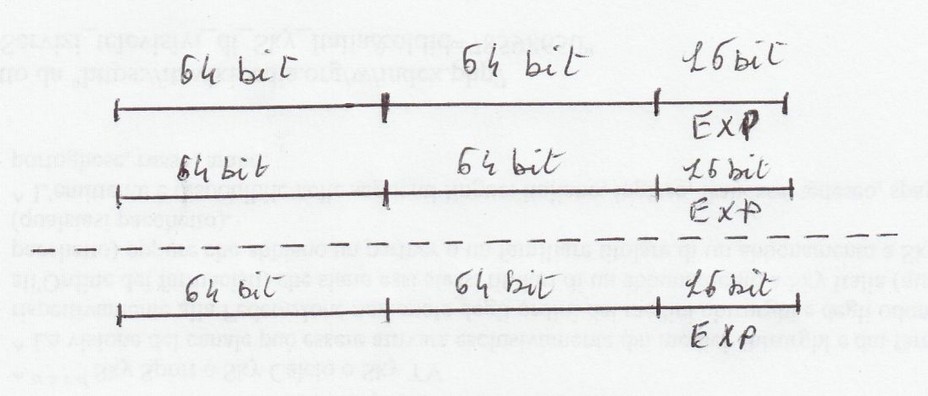
Come si vede sopra per fare una somma a 128 bit con un microcomputer a 64 bit occorre
spezzare il dato in due da 64 bit. Il micromputer effettua la somma dei primi 64 bit e poi i
secondi 64 bit con eventuale riporto e esponente se necessiario.
Arrivando al 35° tutti i 64 bit a destra del dato sono errati, mentre sono corretti tutti i bit
a sinistra. Per cui buttare via i dati a destra trasformando il dato da 128+16 in dato
basic significa che il dato ottenuto è tutto corretto. In questo caso si butta via solo errori.
Il vantaggio di questo metodo è che gli errori si accumulano sui primi 64 bit, che poi verranno
eliminati con la conversione fornendo tutti i 64 bit utili esatti.
Per aumentare la precisione, con lo stesso metodo, si potrebbe passare a una dll da 256+16 bit,
ma con l' attuale velocità dei computer non si avrebbe significativi vantaggi.
Comunque con una dll a 256+16 bit si arriverebbe a calcolare la funzione di Newton sino al 70°
con una precisione di 128 bit, oppure al 99° con una precisione di 64 bit, tutto questo però
solo da un punto di vista teorico.
In ogni caso per arrivare al 99° grado occorre aspettere l' arrivo dei nuovi computer del prossimo
futuro, perchè con gli attuali computer commerciali occorrerebbe un tempo stimato di 1.4 Exp15 anni.