la tecnica - Funzione di Newton
Funzione Polimoniale di Newton a passo costante
Menu principale:
la tecnica
La tecnica delle combinazioni specifica per le funzioni
Prima di entrare nella tecnica delle combinazioni occorre fare una premessa che riguarda l' uso del computer.
Nel computer vi sono quattro operazioni fondamentali (oltre le altre che non prendiamo in considerazione),
esse sono somma, sottazione, moltiplicazione, divisione. Queste quattro operazioni si devono dividere in due
gruppi. Somma e sottrazione e poi moltiplicazione e divisione. Il primo gruppo hanno una bassa probabilità
di errore per cui l' errore lo chiamerò Eb, mentre il secondo gruppo hanno una alta probabilità di errore per
cui lo chiamerò Ea. Per capire la bassa probabilità di errore del primo gruppo basta fare il seguente calcolo.
y = 2 + 3 - 3 = 2
Il risultato è esatto, mentre per il secondo gruppo la seguente formula da :
y = 2 / 3 * 3 = 1.999999999999999999
In questo caso il risultato è diverso dal calcolo teorico che deve essere 2 .
La precisione del computer in BASIC va dalle 15 alle 18 cifre se è con esponente o senza esponente.
Qualcuno dice che l' errore del secondo gruppo è piccolo per cui si può approssimare a 2.
In realtà l' errore commesso dal secondo gruppo è grandissimo se riferito alle esigenze attuali.
Ora prendiamo in considerazione la figura seguente.
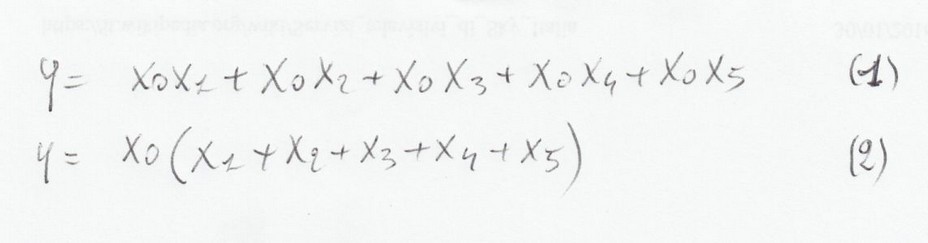
Se ad un matematico fate federe le formule sopra vi dirà che avranno lo stesso risultato, mentre io gli dico
che la formula 1 e 2 danno risultati diversi uno più preciso dell' altro. Questa è la differenza tra la matematica
teorica e la matematica pratica. Nel computer non esiste l' infinito e non sono ammesse licenze poetiche.
Se un matematico desidera continuare con la sua matematica può farlo, ma non si può avvicinare a un
computer, perchè la teoria e una cosa e la pratica un' altra. Se un matematico prende in mano un computer
deve forzatamente togliere l' infinito dalle sue formule sia esse piccole o grandi.
Ora torniamo alle nostre formule e calcoliamo l' errore per capire la formula più precisa.
E1 = 5Ea + 4Eb E2=1Ea +4Eb
Come si può notare la formula numero 2 è la più precisa avendo un errore grande contro cinque grandi.
Da ciò si deduce che quando si scrive una formula non possiamo scriverla a caso solo perchè teoricamente
corretta, ma si deve scriverla con il maggior numero di somme e sottrazioni possibili e un minor numero di
moltiplicazioni e divisioni. Per capire ciò basta pensare che calcolare la funzione di Newton al 33° grado
occorrono 86 miliardi di operazioni (miliardo più miliardo meno) in un tempo di 10 minuti (minuto più
minuto meno) e da un risultato completamente errato. Questo non è dovuto al metodo di calcolo ma
agli errori che si accumulano dovuto alla grande quantità di operazioni. Il massimo grado che si può
calcolare con gli attuali 64 bit è il quattordicesimo, se l'errore è trascurabile come qualcuno sostiene
si dovrebbe arrivare a gradi molto superiori. Sotto vi è il grafico Errori-Gradi dove si può notare
quando gli errori arrivano in modo preponderante.
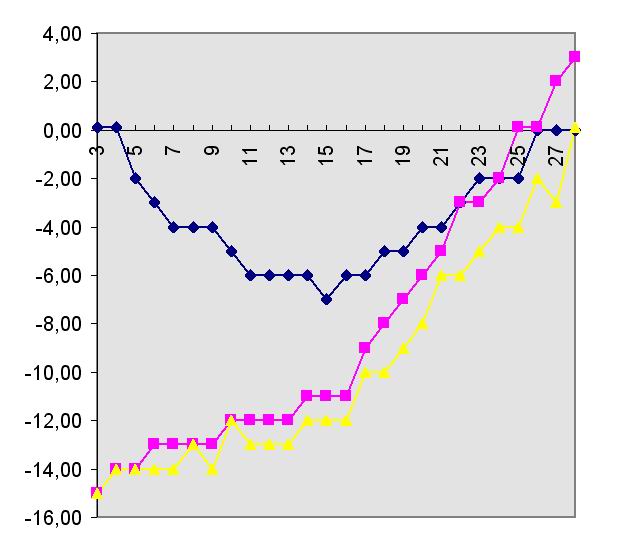
Con questo metodo il tempo di calcolo è lineare e per ogni grado il tempo raddoppia, vedi sotto.

Combinazioni
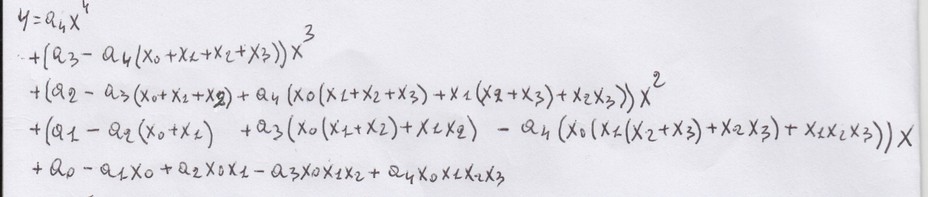
Se abbiamo quattro elementi, per esemio X0 X1 X2 X3 e vogliamo una combinazione da due, tutte le possibili
combinazioni, escludendo se stesso, sono: X0X1 X0X2 X0X3 X1X2 X1X3 X2X3 mentre con gli stessi elementi
una combinazione da tre, sono: X0X1X2 X0X1X3 X0X2X3 X1X2X3. Supponendo di fare la somma di una
combinazione da due con quattro elementi, essa è :
y = X0X1 + X0X2 + X0X3 + X1X2 + X1X3 + X2X3 (a)
Come abbiamo visto sopra per una maggiore precisione dobbiamo privilegiare le somme e sottrazioni al posto
delle moltiplicazioni e divisioni, per cui abbiamo :
y = X0 ( X1 + X2 + X3 ) + X1 ( X2 + X3 ) + X2X3 (b)
Notate bene che mentre per la formula (a) si vede bene che è la somma di una combinazione, non è così
evidente per la formula (b) , ma la formula (a) e (b) sono somme di combinazioni.
Ora facciamo la somma di una combinazione da tre con quattro elementi, essa è:
y = X0X1X2 + X0X1X3 + X0X2X3 + X1X2X3 (c)
y = X0 ( X1X2 +X1X3 + X2X3 ) + X1X2X3 (d)
Y = X0 ( X1 ( X2 +X3 ) + X2X3) ) + X1X2X3 (e)
Come sopra le formule (c) e (e) sono somme di combinazioni. Quando si ha che fare con una formula come la
(e) occorre dire che è un somma di una combinazione da tre con quattro elementi. Come è possibile capirlo?.
Contando gli elementi sino alla somma, in questo caso X0,X1,X2 tre elementi quindi combinazione da tre, mentre
per il numero degli elementi è quattro essendo X0,X1,X2,X3. Le stesse considerazioni vale per la formula (b),
combinazione due - elementi quattro. Ora prendiamo in considerazione il risultato completo della formula di
Newton di quarto grado, vedi sotto.
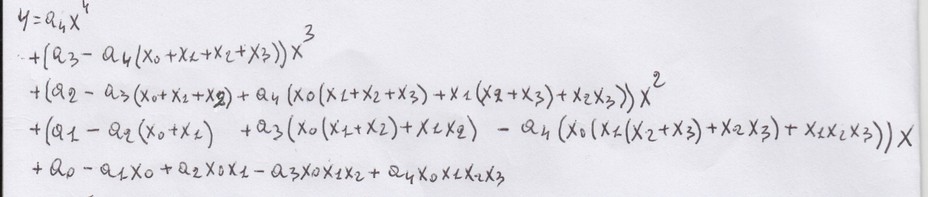
Avendo già studiato la base ora dobbiamo prendere in considerazione ciò che cè scritto dentro le parentesi (c,e).
c è il numero delle combinazioni e è il numero degli elementi
La prima e l' ultima riga, come già visto, non le prendiamo in considerazione perchè hanno regole dedicate.
Il numero delle combinazioni di una riga parte da zero alla prima colonna sino alla fine della riga aumentando
di 1. Per cui alla prima colonna il numero delle combinazioni è zero (e adesso chi glie lo dice ai matematici
che la somma delle combinazioni zero per un numero di elementi n da 1 ? , io no! ).
La seconda colonna ha un numero di combinazioni uno per cui la somma delle combinazioni si riduce alla
somma degli elementi stessi. La prima e la seconda colonna, pur essendo "ricorsive", sono colonne anomale per
cui vanno processate separatamente. La terza colonna della seconda riga è una combinazione da due.
Ora dobbiamo notare che, iniziando dalla prima colonna, la riga finisce quando l' indice di a è uguale al grado.
Il numero degli elementi per ogni combinazione che si prende in considerazione è l' indice di a .
Per esempio la combinazione della terza riga colonna tre c = 2 cioè 3 - 1 mentre il numero degli elementi
deve essere uguale all' indice di a cioè quattro, da cui e = 4 .
Nella terza colonna ci sarà sempre combinazioni da due ma con un numero sempre decrescente di elementi.
Esendo le combinazione con gli elementi "ricorsive" è possibile allargarla senza limitazione.
Per cui il valore di (c,e) è noto una volta stabilito il numero delle combinazioni e il numero degli elementi.
Ora facciamo un esempio come si possa scrivere ciò che cè scritto in (c,e) una volta stabilito il numero
delle combinazioni e il numero degli elementi. Prendiamo c = 4 , e = 6 .
Siccome il numero delle combinazioni è quattro, come visto precedentemente, devo scrivere quattro
elementi con le parentesi, cioè : X0,X1,X2,X3 e aggiungere con la somma gli elementi rimanenti.
a6(4,6) = a6( X0 ( X1 ( X2 ( X3 + X4 + X5 ) +
A questo punto la formula non è finita siamo solo all' inizio.
Ora dobbiamo notare che la combinazione fino a X2 è finita e dobbiamo proseguire.
Con il modo "ricorsivo" dopo il due viene il tre per cui bisogna aggingere X3 con gli elementi rimanenti.
a6(4,6) = a6( X0 ( X1 ( X2 ( X3 + X4 + X5 ) + X3 ( X4 + X5 ) +
con lo stesso ragionamento di prima dopo tre viene quattro, come prima partiamo da X4 con gli
elementi rimanenti.
a6(4,6) = a6( X0 ( X1 ( X2 ( X3 + X4 + X5 ) + X3 ( X4 + X5 ) + X4X5 ) +
La formula non è finita perchè occorre contare le parentesi aperte e chiuse.
Le parentesi aperte sono cinque mentre le chiuse sono tre. Per cui dobbiamo proseguire.
Le parentesi aperte e chiuse con lo stesso numero partono da X1 . Essendo "ricorsivo" dopo X1
viene X2 . Doppiamo partire da X2 con gli elementi rimanenti.
a6(4,6) = a6( X0 ( X1 ( X2 ( X3 + X4 + X5 ) + X3 ( X4 + X5 ) + X4X5 ) + X2 ( X3 ( X4 +X5 ) +
Da notare che il numero delle combinazioni è quattro , per cui occorre sempre contare come visto
sopra il numero degli elementi. In questo caso gli elementi da contare sono X0,X2,X3,X4 prima del
segno più , combinazione da quattro.
Ora dobbiamo finire lo svolgimento di X2. Come sopra dopo X3 viene X4 con gli elementi rimanenti.
a6(4,6) = a6( X0 ( X1 ( X2 ( X3 + X4 + X5 ) + X3 ( X4 + X5 ) + X4X5 ) + X2 ( X3 ( X4 +X5 ) +
X4X5 ) +
Anche in questo caso dopo X2 viene X3 con gli elementi rimanenti .
a6(4,6) = a6( X0 ( X1 ( X2 ( X3 + X4 + X5 ) + X3 ( X4 + X5 ) + X4X5 ) + X2 ( X3 ( X4 +X5 ) +
X4X5 ) + X3X4X5 ) +
In questo caso come sopra gli elementi da contare sono X0,X3,X4,X5 combinazione da quattro .
La formula non è finita perchè dopo X0 arriva X1, con una combinazione ovviamente da quattro
con gli elementi rimanenti.
a6(4,6) = a6( X0 ( X1 ( X2 ( X3 + X4 + X5 ) + X3 ( X4 + X5 ) + X4X5 ) + X2 ( X3 ( X4 +X5 ) +
X4X5 ) + X3X4X5 ) + X1 ( X2 ( X3 ( X4 +X5 ) + X4X5 ) +
Anche in questo caso dopo X2 arriva X3 , con gli elementi rimanenti.
a6(4,6) = a6( X0 ( X1 ( X2 ( X3 + X4 + X5 ) + X3 ( X4 + X5 ) + X4X5 ) + X2 ( X3 ( X4 +X5 ) +
X4X5 ) + X3X4X5 ) + X1 ( X2 ( X3 ( X4 + X5 ) + X4X5 ) + X3 X4 X5 ) +
Come sopra dopo X1 arriva X2 con gli elementi rimanenti, con una combinazione da quattro.
a6(4,6) = a6( X0 ( X1 ( X2 ( X3 + X4 + X5 ) + X3 ( X4 + X5 ) + X4X5 ) + X2 ( X3 ( X4 +X5 ) +
X4X5 ) + X3X4X5 ) + X1 ( X2 ( X3 ( X4 + X5 ) + X4X5 ) + X3 X4 X5 ) + X2X3X4X5 )
La formula è finita. Come avete notato la formula si scrive in modo "ricorsivo" tenendo presente
le combinasioni, gli elementi e proseguendo contando gli indici come si contano i numeri.
Con questo metodo si può scrivere qualsiasi formula partendo dal numero di combinazioni e dal
numero degli elementi. Si tenga presente che il numero delle combinazioni deve essere
sempre inferiore al numero degli elementi.
A questo punto si può scrivere il risutato della formula di Newton di qualsiasi grado
senza effettuare nessun svolgimento come avevo detto inizialmente spiegando così
il salto matematico.