la base - Funzione di Newton
Funzione Polimoniale di Newton a passo costante
Menu principale:
la base
La base per le funzioni sono come le fondamenta per una casa. Prendiamo in considerazione il risultato
delle funzioni di terzo grado, vedi sotto.
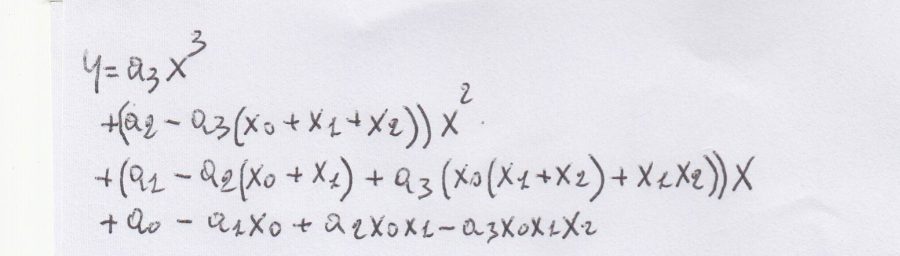
Per prima cosa bisogna notare che il risultato non è stato scritto come mi insegnava il mio professore a scuola
in modo continuo senza nessuna regola. Il risultato va scritto per righe e per colonne tenendo presente il
grado della funzione. Dalla funzione precedente si ricava la figura successiva.
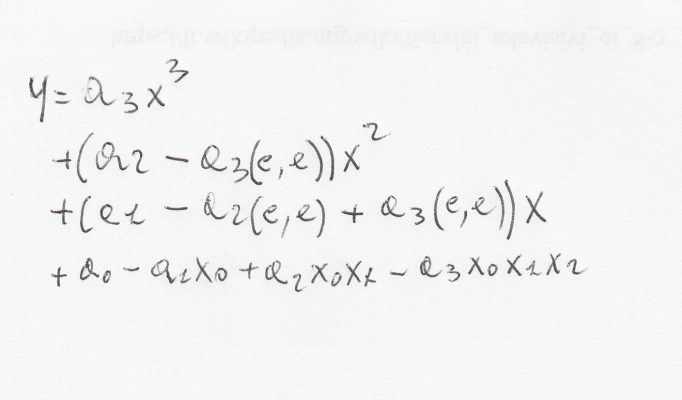
Questa formula è identica alla precedene fatta eccezione per "c,e" tra parentesi che sostituisce i valori precedenti.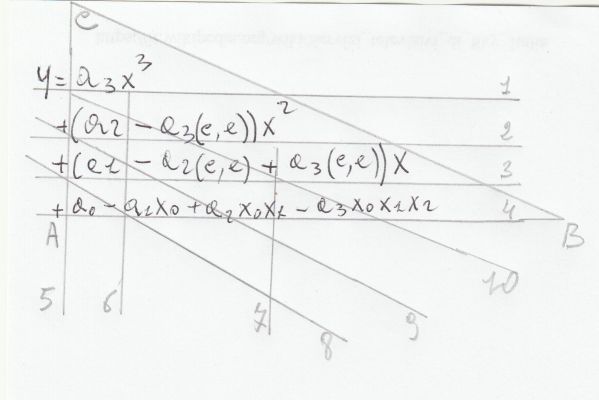
In questa fase dobbiamo concentrarci sulla base e lasciare in seguito ciò che è scritto entro le parentesi (c,e) .
Ora analizziamo la formula per righe e per colonne come si vede sotto.

La prima riga 1 è formata da a3 che rappresenta il grado della funzione in esame.
La riga due 2 parte da a2 (cioè a3-1) e arriva a a3.
La riga tre 3 parte da a1 (cioè a2-1) e arriva a a3.
La prima colonna 5 parte da a3 e arriva a a0 e così via.
A questo punto si può capire che la formula è "ricorsiva" cioè "ricorrente".
Se notate gli indici sia per righe che per colonne e anche trasversali potete notare la sua assoluta linearità.
Per esempio prendiamo la linea trasversale 10 potete notare che rimane sempre a3, così come a2 per la riga 9.
Prendendo in considerazione la struttura della formula questa rimane inalterata all' aumentare dei gradi,
semplicemente diventando più grande. Le ricorrenze sono talmente tante che scrivere la formula più grande
è praticamente impossibile errare. Il triangolo formato dalle lettere A,B,C rimane inalterato all' aumentare dei
gradi, semplicemente diventa più grande. Per cui questo risultato lo chiamato "soluzione triangolare".
La prima riga e l' ultima riga sono "ricorsive" ma seguono regole dedicate. Mentre per il corpo centrale esiste
una sola regola. A questo punto si può vedere la linearità della formula e come allargarla.
Ora partendo dal risultato visto sopra scriviamo la formula di grado superiore senza effettuare lo svolgimento,
ma basandoci semplicemente sugli indici e il modo "ricorsivo" che essi rappresentano.
Si parte dalla riga 1 della figura precedente, essa è a3_X^3 il grado superiore sarà a4_X^4 e quindi la prima riga
è trovata, vedi sotto.
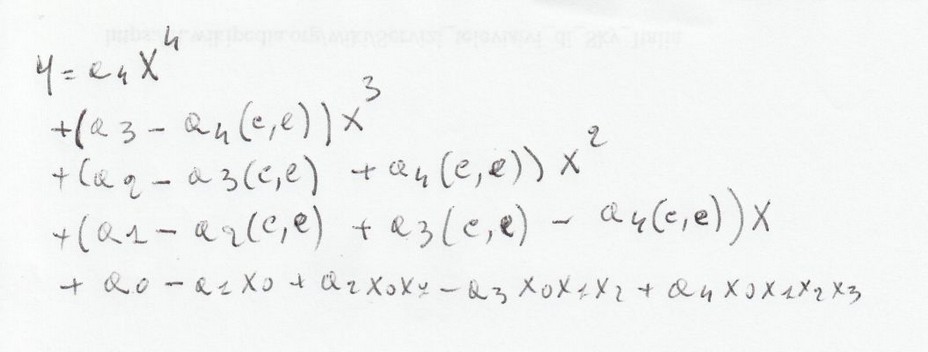
Iniziando da a4 scriviamo gli a con gli appropriati indici della prima colonna, in questo caso da a4 sino a a0.
Questo si puo fare perchè la formula è "ricorsiva". A questo punto scriviamo gli ai(c,e) delle righe eccetto
l' ultima. Ora è la volta del segno davanti a ai(c,e) partendo sempre dal segno meno e alternandolo col più.
Adesso alle righe ottenute mettiame le parentesi e davanti ad esse sempre il segno più. Scriviamo le X in
senzo diagonale partendo dall' alto e diminuendo di grado per ogni riga. Non rimane che scrivere l' ultima riga.
Partendo da a0 già scritto si scrive gli a da a0 a a4 aumentando l' indice, e aggiungendo le x con lo stesso
metodo della formula di partenza. Come potete notare l' ultima riga è identica alla riga di terzo grado con
l' aggiunta di a4x0x1x2x3. Ricordatevi che anche in questa riga i segni sono sempre alternati partendo sempre
dal segno più. Fatto ciò la formula di quarto grado è completa e non abbiamo fatto nessun svolgimento.
A questo punto, per tutti coloro che hanno una minima pratica di programmazione, si può programmare la
base delle funzioni con due semplici For-Next, una per le righe e una per le colonne arrivando sino al 99° grado.